複素数の複素数乗、i^i^i^‥‥の計算
$\dagger\;\;$ 前準備
ここでは、複素数の偏角について、主値 $Arg(\cdot)$ を使い、その範囲は \begin{align*} 0 \leq Arg(\cdot) \lt 2\pi \end{align*} であるとする。したがって、複素対数関数においても、その主値をあたえる関数 $Log(\cdot)$ を使う。その結果、複素数 $\omega$ について \begin{align*} Log(\omega) = \ln{\abs{\omega}} + i\cdot Arg(\omega) \end{align*} となる。もちろん、$i$ は純虚数、$\ln$ は実自然対数関数である。
$\dagger\;\;$ 複素数の複素数乗
数値計算をやりやすくするために、複素数の複素数乗を実数であらわすことを試みよう。なお以下数字文字について、アルファベットは実数、ギリシア文字($\omega, \mu$ など)は複素数を表すものとする。$i$(純虚数)と $\theta$(偏角として使うので実数)は特別である。
$\square\;\; \omega^\mu$
まず、複素対数関数(主値)をもちいると \begin{align*} Log(\omega) = \ln{\abs{\omega}} + i\cdot Arg(\omega) \end{align*} である。ついで複素冪乗関数をもちいれば、 \begin{align*} \omega^\mu = e^{\mu \cdot Log(\omega)} \end{align*} となる。ここで $\omega$ に対して極座標表示 $\omega = re^{i\theta}$ 使う。$r$ は正の実数であり、$0 \leq \theta \lt 2\pi$ であるとする。こうすることによって \begin{align*} \abs{\omega} = r \;, \quad Arg(\omega) = \theta \end{align*} ということになる。したがって、 \begin{align*} Log(\omega) = \ln{r} + i\theta \end{align*} であり、 \begin{align*} \omega^\mu = e^{\mu \cdot Log(\omega)} = e^{\mu (\ln{r} + i\theta)} = e^{\mu \cdot \ln{r}} e^{i\mu\theta} \end{align*} となる。また、実数 $r \;(\gt 0)$ については、$Log(r) = \ln{r} + i\cdot Arg(r) = \ln{r}$ であるから \begin{align*} r^\mu = e^{\mu \cdot Log(r)} = e^{\mu \cdot \ln{r}} \end{align*} となるので、最終的に \begin{align*} \omega^\mu = r^\mu e^{i\mu\theta} \end{align*} という結果が得られる。
$\square\;\; \omega^{c + id}$
$\omega^\mu = r^\mu e^{i\mu\theta}$ において、$\mu := c + id$ と置き換えると、字面は \begin{align*} \omega^{c + id} = r^{c + id} e^{i(c + id)\theta} = r^{c + id} e^{ic\theta} e^{-d\theta} \end{align*} となる。ここで、実数 $r$ の偏角は、主値を採用するので常に $0$ であることと、先ほどみた $Log(r) = \ln{r}$ という関係を使って \begin{align*} r^{c + id} = r^cr^{id} = r^c e^{id \cdot Log(r)} = r^c e^{id \cdot \ln{r}} \end{align*} が得られるから \begin{align*} \omega^{c + id} = r^c e^{id \cdot \ln{r}} e^{ic\theta} e^{-d\theta} = r^c e^{-d\theta} e^{i(d \cdot \ln{r} + c\theta)} \end{align*} ということになる。
$\square\;\; (a + ib)^{c + id}$
$\omega := a + ib$ と置き換えることにしよう。極座標表示 $\omega = re^{i\theta}$ との関係は \begin{align*} r = \sqrt{a^2+b^2} \;, \quad \theta = tan^{-1}\frac{b}{a} \;. \end{align*} この関係を使うと \begin{align} \omega^{c + id} &= (a + ib)^{c + id} = r^c e^{-d\theta} e^{i(d \cdot \ln{r} + c\theta)} \notag \\ &= \left(\sqrt{a^2+b^2}\right)^c e^{-d\theta} e^{i(d \cdot \ln{\left(\sqrt{a^2+b^2}\right)} + c\theta)} = \left(a^2 + b^2\right)^\frac{c}{2} e^{-d\theta} e^{i\left(\frac{d}{2} \cdot \ln{\left(a^2+b^2\right)} + c\theta\right)} \notag \\ &= e^{-d\theta} \left(a^2 + b^2\right)^\frac{c}{2} \left\{ \cos\left(\frac{d}{2} \cdot \ln{\left(a^2+b^2\right)} + c\theta\right) + i\cdot \sin\left(\frac{d}{2} \cdot \ln{\left(a^2+b^2\right)} + c\theta\right) \right\} \label{eq.01} \end{align} と求まって、実部と虚部の数値計算が可能になる。それゆえ、複素平面上にプロットすることができるようになる。
$\square\;\;$ いくつかの検算
- 実数の場合にも成立しているか
$\omega = a,\, \mu = b$ とする。すなわち \eqref{eq.01} において $b = d = 0$ である。また、$\theta$ は $\omega = a$ の偏角の主値であるから、$\theta = 0$ である。したがって、 \begin{align*} a^c = e^0 \left(a^2\right)^\frac{c}{2} \left\{ \cos\left(0 \cdot \ln{a^2} + c \cdot 0\right) + i\cdot \sin\left(0 \cdot \ln{a^2} + c \cdot 0\right) \right\} = \left(a^2\right)^\frac{c}{2} \left\{ \cos 0 + i\cdot \sin 0 \right\} = a^c \end{align*} となり、実数の実数乗がきちんと包含されている。
- $1^i$ は $1$ になっているか
$\omega = 1,\, \mu = i$ である。すなわち \eqref{eq.01} においては、$a = d = 1$ であり $b = c = 0$ である。また、$\theta$ は $\omega = 1$ の偏角の主値であるから、$\theta = 0$ である。
まず、複素冪乗関数で計算すると \begin{align*} 1^i = e^{i\cdot Log(1)} = e^{i (\ln{1} + i\cdot 0)} = e^0 = 1 \;. \end{align*} \eqref{eq.01} でも、やはり \begin{align*} 1^i = e^0 \left(1^2\right)^\frac{0}{2} \left\{ \cos\left(\frac{1}{2} \cdot \ln{\left(1^2\right)} + 0 \cdot 0\right) + i\cdot \sin\left(\frac{1}{2} \cdot \ln{\left(1^2\right)} + 0 \cdot 0\right) \right\} = \left\{ \cos 0 + i\cdot \sin 0 \right\} = 1 \;. \end{align*}
- $i^i$ はいくつか
$\omega = i,\, \mu = i$ である。すなわち \eqref{eq.01} においては、$a = c = 0$ であり $b = d = 1$ である。また、$\theta$ は $\omega = i$ の偏角の主値であるから、$\theta = \pi/2$ である。
まず、複素冪乗関数で計算すると \begin{align*} i^i = e^{i\cdot Log(i)} = e^{i (\ln{1} + i\cdot \frac{\pi}{2})} = e^{-\frac{\pi}{2}} \;. \end{align*} \eqref{eq.01} でも、やはり \begin{align*} i^i = e^{-\frac{\pi}{2}} \left(1^2\right)^\frac{0}{2} \left\{ \cos\left(\frac{1}{2} \cdot \ln{\left(1^2\right)} + 0 \cdot \frac{\pi}{2}\right) + i\cdot \sin\left(\frac{1}{2} \cdot \ln{\left(1^2\right)} + 0 \cdot \frac{\pi}{2}\right) \right\} = e^{-\frac{\pi}{2}} \left\{ \cos 0 + i\cdot \sin 0 \right\} = e^{-\frac{\pi}{2}} \end{align*} となっている。驚くべきことに、$i^i$ は実数になるのである。
$\dagger\;\;$ $i\verb#^# i\verb#^#i \verb#^# \cdots$ を計算する
$i$ の $i$ 乗の $i$ 乗‥‥を計算してみよう。普通に書けば $\displaystyle{ i^{i^{i^{i^i}}} }$ となるが、かなり煩わしいし、第一見難い。なので $i^i \equiv i\verb#^#i$ と記すことにする(プログラミング言語では、この手の書き記し方を採用しているものが多い)。そして、数学の世界の常識では、この「冪演算」は右結合であると決められている。すなわち \begin{align*} i^{i^{i^{i^i}}} = i\verb#^# i\verb#^# i\verb#^# i\verb#^# i = (i\verb#^# (i\verb#^# (i\verb#^# (i\verb#^# i)))) \;. \end{align*} したがって、冪乗の回数をより多くするものについては(無限回も睨んで) \begin{align*} i\verb#^# i\verb#^# i\verb#^# i\verb#^# i \cdots = (i\verb#^# (i\verb#^# (i\verb#^# \cdots (i\verb#^# i)))) \end{align*} とあらわされることになる。
$i\verb#^# i\verb#^# i\verb#^# i\verb#^# i \cdots$ の計算は、今見たように右結合であるから、まず最初に $i\verb#^# i$ を計算し、それを $i$ の肩に乗せて計算し、さらにその結果を $i$ の肩に乗せて、と逐次実行していくことになる。そしてその計算の過程では、$i$ の複素数乗が必要になる。一般形をもとめておこう。 \eqref{eq.01} において $a=0, b=1$ として、$\theta = Arg(i) = \pi/2$ も思い出しておけば \begin{align} i\verb#^# (c + id) = e^{-\frac{\pi}{2}d}\left\{\cos\left(\frac{\pi}{2}c\right) + i\cdot\sin\left(\frac{\pi}{2}c\right)\right\} = e^{-\frac{\pi}{2}d}\cos\left(\frac{\pi}{2}c\right) + i \cdot e^{-\frac{\pi}{2}d}\sin\left(\frac{\pi}{2}c\right) \label{eq.02} \end{align} となる。ここまで来れば、プログラミングは容易い。アルゴリズムの骨格は次のとおり:
この後、gnuplot を使って複素平面上でのグラフ化を考えているので、gnuplot 向けに実部、虚部を出力するプログラム i-pow-i.c を作成した(コンパイル時には数学ライブラリをリンクすることを忘れぬように。gcc ならば -lm オプションである)。10 回ほど繰り返して、各回数での実部、虚部の実数を求めてみると次のようになる。
- $\omega_0 := i\verb#^# i$ とする(そしてそれはすでに、$e^{-\frac{\pi}{2}}$ と求まっている)。
- $\omega_1 := i\verb#^# {\omega_0}$ を \eqref{eq.02} を使って計算する。
- $\omega_n = i\verb#^# {\omega_{n-1}}$ なので、好きな $n$ まで繰り返せば良い。
複素平面上の1点に収束していくような風情がある。 それを確認するために、200 回ほど計算し、各回での複素平面上での点を gnuplot でプロットしたのが次のグラフである (gnuplot のプログラムはi-pow-i.gplt。また利用したDATA は、上の C プログラムで引数を200 として 200 回実行したもの)。# times Re Im # ------------------------------------------------------ 1 0.000000 1.000000 2 0.207880 0.000000 3 0.947159 0.320764 4 0.050092 0.602117 5 0.387166 0.030527 6 0.782276 0.544607 7 0.142562 0.400467 8 0.519786 0.118384 9 0.568589 0.605078 10 0.242365 0.301151
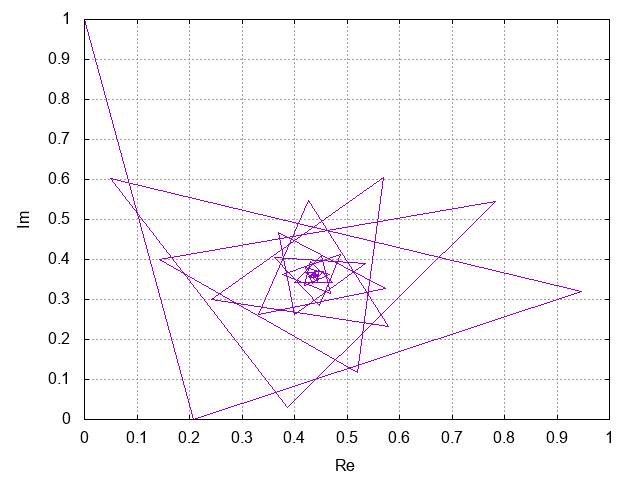
$\dagger\;\;$ $\omega\verb#^# \omega\verb#^#\omega \verb#^# \cdots$ を計算する
虚数単位 $i$ の冪乗シリーズはある点に収束するであろうことが見て取れたが、その他の複素数の冪乗シリーズはどうなるのだろうか?収束するものとしないもの、収束しないとしてもある範囲で振動するものなどが存在するのではあるまいか。
$\omega$ を $n$ 回冪乗したものは \begin{align*} \tau_n(\omega) = \omega\verb#^# \omega\verb#^# \omega\verb#^# \cdots \verb#^#\omega \end{align*} とあらわせる。 帰納的な形であらわせば \begin{align*} \tau_n(\omega) = \omega\verb#^# \tau_{n-1}(\omega) \end{align*} である。 この $\tau_n(\omega)$ が収束するような $\omega$ は複素平面上でどのような分布になっているかが探れればよいのだけれど、さてどのように実装すればいいか。
収束する点と収束しない点を判別し、gnuplot の力を借りてそれぞれ色分けして複素平面の点に色をつけるという作業をすれば、目的のものができるだろう(mandelbrot 集合や julia 集合の描写のようなものを考えている)。収束の判定にちょっと工夫がいるかなと漠然と思っているのだけれど、gnuplot 上で書けるいいプログラムがまだ浮かばない。今後の課題です(実はいったんそれらしきものが出来あがったのだけれど、致命的な欠陥に気がついたので、再度考慮中なのですね)。
$\ddagger\;\;$ references
本文中で利用した複素対数関数や複素冪乗関数などについては、個人的な備忘録雑文として
を書いた。また指数法則についても で雑文化した。こちらの最後の方で、複素数にたいする指数法則の運用方法が簡単にまとめてある。よろしかったら、覗いて見てください。