複素｛指数関数、対数関数｝の世界のさわり

---

---

Table of Contents

• 複素数の表現と複素平面
• 絶対値と偏角
• １価関数と多価関数
• 複素関数の微分
• 複素指数関数
• $\arg(z)$ という偏角関数
• 複素対数関数
• 複素指数関数の一般化と複素冪乗関数
• 主値
• 脚註
• あとがき

---

複素数の表現と複素平面

数学の発展の歴史においての複素数の導入の動機にはいろいろあるのだろうけれど（例えば $x^2 = -1$ を解きたいという動機）、ここではその歴史的意義には目をつぶり、

複素数とは $z = x + iy$ という形で表される数のことである（$x$、$y$ は実数）

という定義を受け入れよう。 $x$ のことを $z$ の実数部分（または実部）、$y$ のことを $z$ の虚数部分（または虚部）といい、次の記号が定められている： \begin{align*} z = x + iy \iff \begin{cases} x \equiv Re(z) \equiv \Re(z) \\ y \equiv Im(z) \equiv \Im(z) \end{cases} \end{align*} $Im(z) = 0$ のときは実数である。 $Re(z) = 0$ のときを純虚数と言ったりもする。 ちなみに、実数以外の複素数を虚数ということもある。 集合記法でこの関係をあらわせば \begin{align*} \set{ \text{複素数} } &= \set{ \text{実数} } \cup \set{ \text{虚数} } \;, \\ \emptyset &= \set{ \text{実数} } \cap \set{ \text{虚数} } \;. \end{align*} ここから、複素数についてあれこれ考える際の、ひとつの「指導原理」が生じてくるように思われる。 それは、$z$ であらわされた複素数が実数 $x$ である場合には、それは実数の世界の数学を壊してはならない、という原理である。 言い換えれば、実数の世界でのある数学的関心事項の一階述語命題 $P(x)$ にたいして、それを複素数の世界に拡張した $P(z)$ は自然で辻褄の合うことが納得できる拡張でなければならない、ということであり、逆に $Q(z)$ にたいしては、$Q(x)$ も実数の世界で辻褄が合わなければならない、という原理である。 例えば、のちに見ることになる複素数の $\cos$ 関数は \begin{align*} \cos(z) = 1 - \frac{1}{2!}z^2 + \frac{1}{4!}z^4 + \cdots \end{align*} であり、$z = x$ とした実数の世界においても \begin{align*} \cos(x) = 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 + \cdots \end{align*} であるから、そのまま拡張されていると読むことができる。 一方で、実数の世界での対数関数については \begin{align*} \log_e x^y = y \log_e x \end{align*} が成立するるけれど、これが複素数の世界になると、複素数の世界の対数関数を $\mathbb{log}_e$ とすれば \begin{align*} \mathbb{log}_e z^w = w \mathbb{log}_e z + i\cdot 2k\pi \quad(k \in \mathbb{Z}) \end{align*} ということになる（これものちに見ることになる）。 余分な $i\cdot 2k\pi$ があらわれてきているが、実数の世界には $i$ というものが「存在しない」と割り切れば、この余分なものも存在しないとみなせて、実数の世界の結果を破壊していないと言えると思う。 それゆえに、実数世界から複素数世界へ自然に拡張されているとも考えられよう。 先に述べた「指導原理」とは、このような事柄を意味したものである、ということを諒解されたい（わたくしはうまく伝えられているだろうか？）。 そしてまた、その拡張が自然であると思えるようになることが学習のひとつのゴールなのであるに違いない。

複素平面という非常に偉大な発明を用いると、$z = x + iy$ は次の図のように、複素平面上の点という幾何学的描像であらわすことが可能になる。

$x = Re(z)$ なので横軸には「実軸」、$y = Im(z)$ なので縦軸には「虚軸」という名前が用意されている。 図からも明らかであるが、これは２次元座標空間と２次元ベクトルの表記に瓜二つだ。 ２次元座標空間のベクトル $\vec{v}$ は、$x$ 成分と $y$ 成分を用いて $\vec{v} = (x, y)$ とかかれることがあるけれど、これを複素平面に翻訳してみると、$z$ は実数成分と虚数成分からなっていて \begin{align*} z = \text{（実数成分,　虚数成分）} = (x, y) = x + iy \end{align*} というように捉えることもできる。 形式は瓜二つであるが、「虚数成分」というものが複素数の特徴を端的にあらわしている。

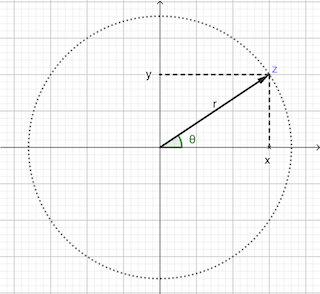
また、幾何的な考察から \begin{align*} & x = r\cos\theta \;,\quad y = r\sin\theta \;, \\ & r = \sqrt{x^2 + y^2} \;, \\ & \theta = \tan^{-1}\frac{y}{x} \;, \end{align*} という関係があることがわかる。 したがって \begin{align*} z = x + iy = r(\cos\theta + i\sin\theta) \end{align*} という表記が可能になる。 $r(\cos\theta + i\sin\theta)$ という表記は「極形式」と言われ、その際の $r,\, \theta$ のことを極座標と言ったりもする。 これらの関係をぐっと睨むと、$z$ と $(x, y)$（ペアという思いを込めている）には１対１の関係があるけれど、 $(r, \theta)$ の $\theta$ には不定性（任意性）があることがわかる。 $\theta$ でも $\theta + 2\pi$、$\theta - 2\pi$ でも同じ複素数 $z$ があらわされている。 図式的に書けば \begin{align*} z \;\longleftrightarrow\; (x, y) \;\longleftrightarrow\; \begin{cases} (r, \theta) \\ (r, \theta \pm 2\pi) \\ \quad\cdots \\ (r, \theta \pm 2n\pi) \\ \quad\cdots \end{cases} \end{align*} この $\theta$ の不定性は、複素数 $z$ が持つ内部自由度と捉えてもいい。 その内部自由度が露出してくる場合が多々あるのが複素関数であり、のちに述べる多価関数となってあらわれてくる （１価関数と多価関数の節を参照）。

---

絶対値と偏角

つぎは、複素数の属性の命名である。

$z = x + iy$ において、「複素数の絶対値」というものを \begin{align*} \abs{z} \equiv \sqrt{x^2 + y^2} = r \end{align*} と定義する。

また、「偏角」というものを、極形式であらわしたときの $\theta$ （上の図での複素数と実軸とのなす角。つまり $\tan^{-1}(y/x)$）として定義する。 先にもふれたけれど、$\theta$ には不定性があって、$\theta - 2\pi$ でも $\theta + 2\pi$ でも $z$ は変わらない。 つまり $z$ に対して偏角はひとつには決まらないものなのである。 そして実際 $\theta + 2k\pi$ 全てが偏角なのである（無限個存在する）。 それゆえ、以下の議論の見通しをよくするために、本稿では $\theta$ という記号に対しては \begin{align*} 0 \le \theta \lt 2\pi \end{align*} というように取り決める。 もう想像がつくと思いますが、要は全体で１周期分に相当する $2\pi$ の範囲をカバーすればいいのだから、この取り決めを $-\pi \lt \theta \le \pi$ や $-\pi/2 \le \theta \lt 3\pi/2$ などとしても一向に差し支えはない。 「matter of taste」または「文脈依存」な取り決めであるから、考察対象に応じて、一番使い勝手の良いものを採用すれば良い。 なので、ここではおそらく一番素直であろうと思われる条件 $0 \le \theta \lt 2\pi$ を課すことにした。

なお、$z = 0$ に対しては、$r = 0$ であるものとし、$z=0$ の偏角というものは定義しないのが習わしである。 $z = x$ つまり実数の偏角は、$x \gt 0$ のときは $\theta = 0$、$x \lt 0$ のときは $\theta = \pi$ となる（複素平面図からあきらかだ）。

---

１価関数と多価関数

ここで少し脇道にそれよう。 関数の値についての考察である。

$\square$ 関数値による分類

$y = x^2 \;\;(-\infty \lt x \lt \infty)$ という関数では、$x$ の値を特定すればそれに対応する関数値 $y$ がピタリとひとつ決まる。 $y = x^3 \;\;(-\infty \lt x \lt \infty)$ についても同様。 $y = \cos(x) \;\;(-\infty \lt x \lt \infty)$ という周期関数でも、$x$ を特定すれば関数値 $y$ もひとつに決まる。 このような関数を「１価関数」と呼ぶことになっている。複素数まで範囲を広げて定義化すれば

１価関数 $f$ とは、$w = f(z)$ とあらわしたとき、$z$ を決めれば、関数値 $w$ がひとつに定まる関数のことをいう

となる。 上記 $z$ は独立変数、$w$ は従属変数と言われることはおなじみである。 さらに細かいことを言えば、関数であるのだからその独立変数の範囲すなわち定義域を明らかにし、その定義域において１価である、ということにするのが本格派であろうけれど、ここでは鷹揚に構えました。

混同してはならないことは、１価関数は、必ずしも $x$ と $y$ との１対１対応を意味していない、ということである。 $y = x^2$ や周期関数 $y = \cos(x)$ の例からもそれは明らかだ。 逆に、１対１対応ならば、１価関数であることはもちろんである。

しからば、次のような関数はどうか？ \begin{align*} y = f(x) = \left[\text{独立変数 $x$ の平方根をもとめる}\right](x) \quad(x \gt 0) \end{align*} $x$ を決めると $y$ には $\sqrt{x}$ と $-\sqrt{x}$ の二つの値が存在し、ひとつには決まらない。 これは、$y = x^2$ の逆関数のようにも見えるが、現代では、こういうものを関数とは呼ばないらしい。 それは、$x$ を決めても $y$ がひとつに決定されないことに理由があるようだ。 $y=x^2$ の逆関数は定義できない、と物の本には記述されている。 ある種の厳密さの反映なのかもしれないが、詳細については不勉強であるので、ここでは物の本の額面通りに受け取っておくことにしよう。 しかし、逆関数が定義できなくても、「逆関係」にあることは納得できる。 「逆関係」が関数たるか、というところに問題の焦点がある。

さらに。 $\cos$ の逆関係 $y = \cos^{-1}(x)$ はどうか？ これは様々な方面で、$y = \cos(x)$ の逆関数として当たり前に使われる関数であるけれど、実はそこに「値域のからくり」があるのである。 つまりこの逆関数が１価関数となるように値域を調整して利用しているのである。 通常は、$0 \le y \le \pi$ と制限をして、$y = \cos^{-1}(x)$ を考え、それで万事がうまくいくようになる（ついでに言えば、$\cos$ の逆関係を考えている以上、定義域は $-1 \le x \le 1$ にしかなり得ない）。 その値域の制限を取り払って、$-\infty \lt y \lt \infty$ という値域で $\cos^{-1}$ という関数を見直すと、 $\cos(0) = \cos(2\pi) = \cos(-2\pi) = 1$ などという事実から \begin{align*} \cos^{-1}(1) = \begin{cases} \cdots \\ -2\pi \\ 0 \\ 2\pi \\ \cdots \end{cases} \end{align*} となる。 つまり、$y = \cos^{-1}(x)$ という関数では、$x$ を決めても $y$ は複数存在しているのである （それも無限個。グラフはこんな感じ）。

このような関数が「多価関数」と呼ばれる関数である。これも定義化しておこう。

多価関数 $f$ とは、$w = f(z)$ とあらわしたとき、$z$ を決めても、複数の関数値 $w_1, w_2, \ldots$ が存在する関数のことをいう

以上のことから、関数 $f$ が１価関数であっても、その逆関係が１価関数であるとはかぎらないことがわかってくる。 逆関係が１価関数になるのは、元の関数の定義域と値域において１対１対応が成立している場合にかぎられるのである。　

$\square$ 集合記法の利用

$w = f(z)$ を多価関数とすると、独立変数 $z$ の各々について \begin{align*} f(z) = \begin{cases} w_1 \\ w_2 \\ \cdots \\ w_n \\ \cdots \end{cases} \end{align*} と複数の値（有限個でも無限個でもかまわない）が対応することになる。 これを集合の記号を利用して、 \begin{align*} f(z) = \set{w_1,\, w_2,\, \ldots,\, w_n,\, \ldots} = \set{w_n \mid n \in \mathbb{N}} \end{align*} と記してみる。 多価関数どうしの演算を考える場合にこの表記が便利なときもあるので、その性質と計算記法を少し整理してみようと思う。

• 加法

  数を加えることの意味は、集合の各要素すべてにその数を加えるということである： \begin{align*} \alpha + f(z) = \set{\alpha + w_1,\, \alpha + w_2,\, \ldots,\, \alpha + w_n,\, \ldots} \end{align*}

• 乗法

  数を掛けることの意味は、集合の各要素すべてにその数を掛けるということである： \begin{align*} \alpha \cdot f(z) = \set{\alpha w_1,\, \alpha w_2,\, \ldots,\, \alpha w_n,\, \ldots} \end{align*}

• 多価関数どうしの相等

  多価関数 $f(z)$ と $g(z)$ が等しいということは、 \begin{align*} & f(z) = \set{w_1,\, w_2,\, \ldots,\, w_n,\, \ldots} = \set{w_n \mid n \in \mathbb{N}} \\ & g(z) = \set{w^\prime_1,\, w^\prime_2,\, \ldots,\, w^\prime_m,\, \ldots} = \set{w^\prime_m \mid m \in \mathbb{N}} \end{align*} であるときに、集合の相等としての \begin{align*} \set{w_n \mid n \in \mathbb{N}} = \set{w^\prime_m \mid m \in \mathbb{N}} \end{align*} が成り立つときである。 簡単に言えば、両方の集合の要素が同じである、ということだ。

• 多価関数どうしの加法

  $f(z)$ と $g(z)$ の加法は、各々の要素をすべて加え合わせて、最後に重複している要素をひとつにする（集合要素化）という行為である。 \begin{align*} & f(z) = \set{w_1,\, w_2,\, \ldots,\, w_n,\, \ldots} = \set{w_n \mid n \in \mathbb{N}} \\ & g(z) = \set{w^\prime_1,\, w^\prime_2,\, \ldots,\, w^\prime_m,\, \ldots} = \set{w^\prime_m \mid m \in \mathbb{N}} \end{align*} であるとすれば、 \begin{align*} f(z) + g(z) &= \set{w_1,\, w_2,\, \ldots,\, w_n,\, \ldots} + \set{w^\prime_1,\, w^\prime_2,\, \ldots,\, w^\prime_m,\, \ldots} \\ &= \begin{Bmatrix} w_1 + w^\prime_1,\, w_1 + w^\prime_2,\, \ldots,\, w_1 + w^\prime_m,\, \ldots\\ w_2 + w^\prime_1,\, w_2 + w^\prime_2,\, \ldots,\, w_2 + w^\prime_m,\, \ldots\\ \cdots\cdots \\ w_n + w^\prime_1,\, w_n + w^\prime_2,\, \ldots,\, w_n + w^\prime_m,\, \ldots \\ \cdots\cdots \end{Bmatrix} \end{align*} であり、最後の結果において重複するものがあればそれをひとつにした結果となる。

わかりやすいと思われる有限個の具体例をあげてみよう。 \begin{align*} &f(z) = \set{2,\, 4,\, 6,\, 8} \\ &g(z) = \set{1,\, 2,\, 3} \\ \end{align*} であるときは、 \begin{align*} f(z) + g(z) &= \set{2,\, 4,\, 6,\, 8} + \set{1,\, 2,\, 3} \\ &= \begin{Bmatrix} 2+1,\, 2+2,\, 2+3, \\ 4+1,\, 4+2,\, 4+3, \\ 6+1,\, 6+2,\, 6+3, \\ 8+1,\, 8+2,\, 8+3 \end{Bmatrix} = \begin{Bmatrix} 3,\, 4,\, 5, \\ 5,\, 6,\, 7, \\ 7,\, 8,\, 9, \\ 9,\, 10,\, 11 \end{Bmatrix} \\ &= \set{3,\, 4,\, 5,\, 6,\, 7,\, 8,\, 9,\, 10,\, 11} \end{align*} である。

もう一つの例として \begin{align*} & f(z) = \set{w + 2n\pi \mid n \in \mathbb{N}} \\ & g(z) = \set{w^\prime + 2m\pi \mid m \in \mathbb{N}} \end{align*} という形であらわされる２つの多価関数の和を考えてみる。 各々の集合の要素を具体的に書き下すと \begin{align*} & f(z) = \set{w,\, w+2\pi,\, w+4\pi,\, \cdots} \\ & g(z) = \set{w^\prime,\, w^\prime+2\pi,\, w^\prime+4\pi,\, \cdots} \end{align*} となるから、 \begin{align*} f(z) + g(z) &= \set{w,\, w+2\pi,\, w+4\pi,\, \cdots} + \set{w^\prime,\, w^\prime+2\pi,\, w^\prime+4\pi,\, \cdots} \\ &= \begin{Bmatrix} w + w^\prime,\, w + w^\prime+2\pi,\, w + w^\prime+4\pi,\, \cdots \\ w + w^\prime+2\pi,\, w + w^\prime+4\pi,\, \cdots \\ w + w^\prime+4\pi,\, \cdots \\ \cdots\cdots \end{Bmatrix} \end{align*} であり、ここから重複している要素をひとつにまとめると \begin{align*} f(z) + g(z) = \set{w + w^\prime,\, w + w^\prime+2\pi,\, w + w^\prime+4\pi,\, \cdots} = \set{w + w^\prime + 2k\pi \mid k \in \mathbb{N}} \;. \end{align*}

この計算は、 \begin{align*} f(z) + g(z) &= \set{w + 2n\pi} + \set{w^\prime + 2m\pi} \\ &= \set{w + w^\prime + 2n\pi + 2m\pi} \\ &= \set{w + w^\prime + 2(n+m)\pi} \end{align*} として、$n+m$ でもすべての自然数がまかなえることを使って \begin{align*} = \set{w + w^\prime + 2k\pi \mid k \in \mathbb{N}} \end{align*} と簡略してあらわされることもある。 $f(z)$ と $g(z)$ について $n,\, m$ と異なるものを使うのがひとつのテクニックである。 集合のようなものを相手にするときには、それを表現するパラメタには異なる文字を使う方が紛れがない。 両方に $n$ を使ってしまうと、上記の計算において $2n\pi + 2n\pi = 4n\pi$ という計算をしてしまいがちで、これだと漏れが生じてしまうからである（$4\pi$ の $n$ 倍になってしまうので）。

さらに上で述べた加法の記法を使うと \begin{align*} &f(z) = \set{w + 2n\pi \mid n \in \mathbb{N}} = w + \set{2n\pi \mid n \in \mathbb{N}} \\ &g(z) = \set{w^\prime + 2m\pi \mid m \in \mathbb{N}} = w^\prime + \set{2m\pi \mid m \in \mathbb{N}} \end{align*} とあらわせるから \begin{align*} f(z) + g(z) = w + \set{2n\pi} + w^\prime + \set{2m\pi} \end{align*} となり、集合として $\set{2n\pi \mid n \in \mathbb{N}} + \set{2m\pi \mid m \in \mathbb{N}} = \set{2k\pi \mid \in k \in \mathbb{N}}$ であることはあきらかだから \begin{align*} = w + w^\prime + \set{2k\pi \mid k \in \mathbb{N}} = \set{w + w^\prime + 2k\pi \mid k \in \mathbb{N}} \;. \end{align*}

なおこの計算は、一般には、わざわざ集合の記法を用いずに直接に \begin{align*} &f(z) = w + 2n\pi \quad(n \in \mathbb{N}) \\ &g(z) = w^\prime + 2m\pi \quad(m \in \mathbb{N}) \\ \\ &f(z) + g(z) = w + 2n\pi + w^\prime + 2m\pi = w + w^\prime + 2(n+m)\pi = w + w^\prime + 2k\pi \quad(k \in \mathbb{N}) \end{align*} と書かれることもある。 というか、この書き方で説明してある教科書の方が多いようである。 代数的操作と馴染みやすい、というのがその理由であると勝手に推察している。 もちろんその背景にはここで述べた集合の意味合いが隠されている。 なぜならば、$n + m = k$ とするところは、集合的に考えないと導けない。 しかしながら、わざわざそれを表に出すまでもあるまい、という姿勢なのだろう。 最も簡略化された書き方だと思う。

$\square$ 多価関数を含む式（１階述語命題）

多価関数 $f(z) = \set{w_1,\, w_2,\, \ldots,\, w_n,\, \ldots}$ が何らかの式の中にあらわれた時、それは、「各々の関数値 $w_i$ すべてに対して」という事を意味している、ととらえる。

先の多価関数の加法や乗法の記法で見たように \begin{align*} &\alpha + f(z) = \set{\alpha + w_1,\, \alpha + w_2,\, \ldots} \\ &\alpha f(z) = \set{\alpha w_1,\, \alpha w_2,\, \ldots} \end{align*} となっていた。これを各 $w_k$ に注目してみると \begin{align*} \alpha + f(z) &\quad\Longrightarrow\quad \forall n\;(\alpha + w_n) \\ \alpha f(z) &\quad\Longrightarrow\quad \forall n\;(\alpha w_n) \end{align*} という視野を手に入れることができる。 この手の話になると、一階述語論理の言葉を借用するのが簡便である。 すなわち、１階述語命題 $P$ に対して $P(f(z))$ とあれば、 \begin{align*} P(f(z)) \quad\Longrightarrow\quad \forall n\; P(w_n) \end{align*} と諒解するのである。 こののち、多価関数を用いた関数表現がそれなりに出てくるが、そのとらえかたの基本はこの諒解である。

$\square$ 複素数の表記方法再び

先の複素数の表記方法を関数とみなすと、 \begin{align*} & z = f(x, y) = x + iy \;, \\ & z = g(r, \theta) = r(\cos\theta + i\sin\theta) \;, \end{align*} であるから、独立変数のペア $(x, y)$ や $(r, \theta)$ を決めれば、$z$ も一つに決まる。 つまりこれらは１価関数である。 ではその逆関係はどうなのだろうか？

実数の $x$-$y$ 平面（２次元平面）と複素平面との間の関数関係は

という幾何学的描像から $z$ と $(x,y)$ には１対１の関係が見て取れる。 それゆえ逆関係をあらわす \begin{align*} (x, y) = \left[\text{独立変数 $z$ の実部と虚部を求める}\right](z) \end{align*} という関数は、１価関数である。

しかしながら、実数の $r$-$\theta$ 平面（２次元平面）と複素平面との間の関数関係は、

という描像から明らかなように、$\theta$ でも $\theta + 2\pi$ でも（そして $\theta + 2k\pi$ でも）同一の複素数 $z$ をあらわすことが可能である。 したがってその逆関係をあらわす関数 \begin{align*} (r, t) = \left[\text{独立変数 $z$ の絶対値と偏角を求める}\right](z) \end{align*} は、多価関数なのである（$r$ は絶対値、$t$ は偏角）。 偏角の不定性がその多価関数化をもたらしている。 これを「複素数の内部自由度のあらわれ」とわたくしは名付けたいのですね。

---

複素関数の微分

複素指数関数を考えるときに微分操作が必要になるので、唐突感はいなめないけれども、ここで複素関数の微分についてまとめておく。 といっても、数の実体が複素数にまで拡張されただけで、字面的には実数の場合とまったく同じである（というか、そのように作られている？）。

複素関数 $f(z)$ にも $z$ による微分が定義でき、それを基に導関数、$n$ 階導関数（もちろん $n$ は自然数）が導出される。 導関数の記法は実関数のときと同様に \begin{align*} \frac{df(z)}{dz} \equiv f^\prime(z) \;, \quad \frac{d^2f(z)}{dz^2} \equiv f^{\prime\prime}(z) \;, \quad\ldots\;,\quad \frac{d^nf(z)}{dz^n} \equiv f^{\prime\prime \cdots \prime}(z) \equiv f^{(n)}(z) \end{align*} などであらわされる。 また $\abs{z - \alpha} \lt \rho$ で $f(z)$ が正則であれば（そうそう、正則という単語は初出であるけれど、難しいことは棚に上げて「健康」とか「筋がいい」と言っても問題ないだろう） \begin{align*} f(z) = f(\alpha) + \frac{f^\prime(\alpha)}{1!}(z-\alpha) + \frac{f^{\prime\prime}(\alpha)}{2!}(z-\alpha)^2 + \cdots = \sum_{n=0}^\infty\frac{f^{(n)}(\alpha)}{n!}(z-\alpha)^n \quad(0! \equiv 1) \end{align*} とテーラー展開が定義できることが判明している。 それゆえマクローリン展開も存在して、 \begin{align*} f(z) = f(0) + \frac{f^\prime(0)}{1!}z + \frac{f^{\prime\prime}(0)}{2!}z^2 + \cdots = \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}z^n \;. \end{align*}

合成関数の微分、いわゆる微分の chain rule も実関数の場合と同様に実行できる。 関数 $f(w)$ において、$w$ が $z$ の関数つまり $w = w(z)$ となっている場合には、$f(w) = f(w(z))$ となって \begin{align*} \frac{df}{dz} = \frac{df}{dw} \frac{dw}{dz} \end{align*} というように微分の chain rule が成り立つ。

ここでは結果だけを記したけれど、どうしてこのようなことになっているのかへ深入りするには、きちんとした教科書にあたるべし、である。

---

複素指数関数

$\square$ 定義と構築

$f(z) = e^z$ という関数を考える。 この関数を複素指数関数と呼ぶ。 これについては、今のところ $e = 2.718\cdots$ の $z$ 乗という意味ではなく、単なる関数記号と捉えておくのが賢明だ。 それが $e = 2.718\cdots$ の $z$ 乗と等しくなっていることが、のちに一般の指数関数を導き出すことで判明するけれど、とにかく今は、とある関数の簡略的表記であると認識しておこう（様々な教科書にも、似たような注釈が書いてある）。

さて、どのような出発点から、複素指数関数を考察するか。 実指数関数の定義を自然に拡張していく道筋と、導関数が不変であることから出発する道筋が考えられたので、その各々の道筋をなぞっていってみることにする。

$\bullet$ 実指数関数の定義を自然に拡張していく道筋

この道筋での複素指数関数の定義は、実指数関数の変数を複素数に拡張して \begin{align*} f(z) = e^z = 1 + \frac{z}{1!} + \frac{z^2}{2!} + \cdots = \sum_{n=0}^\infty\frac{z^n}{n!} \quad(0! \equiv 1) \end{align*} というものになる。 この定義は $e^0 = 1$ を内包している。 第 $k$ 項を $e_k := z^k/k!$ とあらわすと（$e_0 = 1$） \begin{align*} e^z = e_0 + e_1 + e_2 + \cdots = \sum_{n=0}^\infty e_n \end{align*} となる。 これを微分してみよう。 項別に微分できるものとして（項が無限個あるので、おそらくなにか条件が必要だとおもわれるけど、それはいまおいておきたい）、 \begin{align*} \frac{de_k}{dz} = \frac{k z^{k-1}}{k!} = \frac{z^{k-1}}{(k-1)!} = e_{k-1} \end{align*} となることから \begin{align*} \frac{d e^z}{dz} = \frac{de_0}{dz} + \frac{de_1}{dz} + \frac{de_2}{dz} + \cdots = 0 + e_0 + e_1 + \cdots = e^z \end{align*} と、まるでヒルベルトのホテルから退場するかのように^[1]、結果が $e^z$ そのものになる。

$\bullet$ 導関数が不変であることから出発する道筋

こちらの道筋では、やはり実指数関数での事実を拡張して \begin{align*} \frac{de^z}{dz} = e^z \end{align*} が成り立つことを複素指数関数の定義とする。 この定義と $e^0 \equiv 1$ という指数に関する大原則の定義から \begin{align*} f^{(n)}(z) = \frac{d^n}{dz^n}e^z = e^z \;, \quad f^{(n)}(0) = \left.\frac{d^n}{dz^n}e^z\right|_{z=0} = e^0 = 1 \quad (\text{for all }n) \end{align*} という性質が導き出される。 したがってマクローリン展開を実行すると \begin{align*} f(z) = e^z = 1 + \frac{z}{1!} + \frac{z^2}{2!} + \cdots = \sum_{n=0}^\infty\frac{z^n}{n!} \quad(0! \equiv 1) \;. \end{align*} となる。

結局の所、どちらの道筋でいっても、定義とするのか結果とするかの違いはあれこそ、得られる事柄は同じなのである。 どちらを好むかは、やはり、matter of taste としかいいようがないのではあるまいか。 わたくしはそう想像するのであるけれど、数学的正義（そんなものがるとして）はどちらに軍配をあげるのだろう？

複素関数らしさが表出してくるのははここからである。 $g(z) = e^{iz}$ として、この $g(z)$ にたいしてマクローリン展開を実行する。 その際に合成関数の微分法を使う。 最初のいくつかを具体的に書いてみると \begin{alignat*}{2} & g(z) = e^{iz} & &\quad\therefore\; g(0) = 1 \;, \\ & \frac{dg}{dz} = i \cdot e^{iz} & &\quad\therefore\; \left.\frac{dg}{dz}\right|_{z = 0} = i \;, \\ & \frac{d^2g}{dz^2} = i \cdot i \cdot e^{iz} = - e^{iz} & &\quad\therefore\; \left.\frac{d^2g}{dz^2}\right|_{z = 0} = -1 \;, \\ & \frac{d^3g}{dz^3} = -i \cdot e^{iz} & &\quad\therefore\; \left.\frac{d^3g}{dz^3}\right|_{z = 0} = -i \;, \\ & \frac{d^4g}{dz^4} = -i \cdot i \cdot e^{iz} = e^{iz} & &\quad\therefore\; \left.\frac{d^4g}{dz^4}\right|_{z = 0} = 1 \end{alignat*} となる。 この計算結果を順次利用して、実数部分と虚数部分を整理すると、 \begin{align*} e^{iz} &= 1 + \frac{i}{1!}z - \frac{1}{2!}z^2 - \frac{i}{3!}z^3 + \frac{1}{4!}z^4 + \cdots \\ &= \left(1 - \frac{1}{2!}z^2 + \frac{1}{4!}z^4 + \cdots \right) + i\left(\frac{1}{1!}z - \frac{1}{3!}z^3 + \frac{1}{5!}z^5 + \cdots \right) \end{align*} となる。 この結果は、$f(iz) = e^{iz}$ として $iz$ を丸ごとマクローリン展開に代入、さらに $(iz)^n = i^n z^n$ という指数法則を利用すれば \begin{align*} e^{iz} &= 1 + \frac{iz}{1!} + \frac{(iz)^2}{2!} + \frac{(iz)^3}{3!} + \frac{(iz)^4}{4!} + \cdots \\ &= \left(1 - \frac{1}{2!}z^2 + \frac{1}{4!}z^4 + \cdots \right) + i\left(\frac{1}{1!}z - \frac{1}{3!}z^3 + \frac{1}{5!}z^5 + \cdots \right) \notag \\ \end{align*} という手順でも求めることができる。 合成関数の微分を持ち出すことは、少々大仰だったかもしれない。 けれども、複素数の範囲においてもこの指数法則 $(iz)^n = i^n z^n$ を無条件に所与の事実として認めて良いのかが若干疑問であったので（もちろんそれは正当な事実である）、第一感として、合成関数による手順の採用にいたったのですね。 と言いながら、複素数でも合成関数の微分が使える、ということは所与の事実としている。 勝手なものである。

$\square$ 基本指数法則

$f(z) = e^z$ について $f(z + w)$ を考えて、それをテーラー展開してみよう。 $f^{(n)}(z) = f(z) = e^z$ であることを利用すれば \begin{align*} f(z + w) &= f(z) + \frac{f^\prime(z)}{1!}w + \frac{f^{\prime\prime}(z)}{2!}w^2 + \cdots \\ &= \sum_{n=0}^\infty \frac{f^{(n)}(z)}{n!}w^n = \sum_{n=0}^\infty \frac{f(z)}{n!}w^n = f(z)\sum_{n=0}^\infty \frac{w^n}{n!} \\ &= f(z)f(w) \end{align*} すなわち \begin{align*} e^{z + w} = e^z e^w \end{align*} となって、基本指数法則が成り立つことが導き出される。

ご多分に漏れず、テーラー展開などという大仰な（？）仕掛けをもちいない導出方法もある。 \begin{align*} e^z e^w = \sum_{n=0}^\infty \frac{z^n}{n!} \sum_{m=0}^\infty \frac{w^m}{m!} = \sum_{n=0}^\infty\sum_{m=0}^\infty \frac{z^n w^m}{n! m!} \end{align*} となるので、ここでこの２重の和の取り方にひと工夫を入れる。 無限級数であるから、項別に取り扱うことに対してはデリケートであり微妙な部分が一般には存在するけれども、ここはひとつおおらかに行ってみよう。 上の式の和の取り方は

(1) $m$ を $0$ から $\infty$ までとり、そのあとで $n$ を $0$ から $\infty$ までとる

というやりかたである。 これを

(2) $n + m = k$ として、それぞれの $k$ に対しての $n, m$ の組み合わせをとる

というものに変更する。 少し具体的に書き下してみると \begin{align*} &k = 0 \rightarrow n = 0 \;, m = 0 \;, \\ &k = 1 \rightarrow \begin{cases} n = 0 \;, m = 1 \\ n = 1 \;, m = 0 \end{cases} \;, \\ &k = 2 \rightarrow \begin{cases} n = 0 \;, m = 2 \\ n = 1 \;, m = 1 \\ n = 2 \;, m = 0 \end{cases} \;, \\ &\cdots\cdots \end{align*} ということになるから、(2) の方法であっても結局はすべての $n,\, m$ についての和をとっていることになっている。 漏れは生じていない。 つまりこの２重和は \begin{align*} \sum_{n=0}^\infty\sum_{m=0}^\infty \quad\longrightarrow\quad \sum_{k=0}^\infty\sum_{n=0}^k \end{align*} というように分解することができるのである。 $m$ はどこへ行ったか？ それは $n + m = k$ から $m = k - n$ という関係に隠されてしまっている。 したがって \begin{align*} e^z e^w &= \sum_{n=0}^\infty\sum_{m=0}^n \frac{z^n w^m}{n! m!} = \sum_{k=0}^\infty\sum_{n=0}^k \frac{z^n w^{k-n}}{n! (k-n)!} \\ &= \sum_{k=0}^\infty\sum_{n=0}^k \frac{k!}{k!} \frac{1}{n! (k-n)!} z^n w^{k-n} = \sum_{k=0}^\infty \frac{1}{k!} \sum_{n=0}^k \frac{k!}{n! (k-n)!} z^n w^{k-n} \\ &= \sum_{k=0}^\infty \frac{1}{k!} (z + k)^k = e^{z+w} \end{align*} となり基本指数法則の成立が示される（最後に２項定理を適用した）^[2]。

もちろん逆方向、すなわち $(z + w)^k$ を２項展開するところから始めて結論として $e^ze^w$ を導き出すことも可能なはずである。 実際にやってみると、まず２項定理の展開から \begin{align*} (z+w)^k = \sum_{n=0}^k \binom{k}{n}z^n w^{k-n} = \sum_{n=0}^k \frac{k!}{(k-n)! n!} z^n w^{k-n} \end{align*} であるので \begin{align*} \sum_{k=0}^\infty \frac{1}{k!}(z+w)^k = \sum_{k=0}^\infty \frac{1}{k!} \sum_{n=0}^k \frac{k!}{(k-n)! n!} z^n w^{k-n} = \sum_{k=0}^\infty \sum_{n=0}^k \frac{1}{(k-n)! n!} z^n w^{k-n} \end{align*} となる。 ここまではいい。 そして $m = k - n$ としたくなるのだが、ここでふんずまった。 形式だけ書き換えると \begin{align*} = \sum_{k=0}^\infty \sum_{n=0}^k \frac{1}{m! n!} z^n w^m \end{align*} なのだけれど、ここで \begin{align*} \sum_{k=0}^\infty\sum_{n=0}^k \quad\longrightarrow\quad \sum_{n=0}^\infty\sum_{m=0}^\infty \end{align*} ということがうまく諒解できなかった。 逆方向つまり最初のやり方はすんなり納得できたのに。 そしてその納得を得たのちだと、この方向の変形も諒解できてきた。 不思議な個人的体験である（どうして最初のやり方の方がすんなりと腑に落ちるのだろう？）。

ともかく、$e^{z+w} = e^ze^w$ である。 これから \begin{align*} e^ze^{-z} = e^{z-z} = e^0 = 1 \iff e^{-z} = \frac{1}{e^z} \end{align*} という重要な関係も求まる。

$\square$ 複素三角関数

さてここでもまた、とある関数を、複素三角関数として定義する。 このような関数名を使う背景には、実関数の場合にそっくりな関数が存在しているという事実があるからである。 それゆえ、実数の世界の自然な拡張であり、実数の世界の数学を壊さないという「指導原理」にも沿うことになる。 定義する関数は次の通り： \begin{align*} &\cos(z) \equiv 1 - \frac{1}{2!}z^2 + \frac{1}{4!}z^4 + \cdots \;, \\ &\sin(z) \equiv \frac{1}{1!}z - \frac{1}{3!}z^3 + \frac{1}{5!}z^5 + \cdots \;. \end{align*} この複素三角関数を使えば、先に求めた $e^{iz}$ が \begin{align*} e^{iz} = \cos(z) + i\sin(z) \end{align*} となる。 $z$ に実数を採用する、つまり、$z = \theta \;\;(\theta \in \mathbb{R})$ とすると \begin{align*} e^{i\theta} = \cos\theta + i\sin\theta \end{align*} となって、著名な「オイラーの公式」（「オイラーの贈り物」という人達もいる）が導き出される。

$\square$ 複素数の新たな表記法と複素指数関数の周期性

オイラーの公式を使うと \begin{align*} z = x + iy = r(\cos\theta + i\sin\theta) = re^{i\theta} \end{align*} というもうひとつの複素数の表記方法が得られる（この形も極形式と呼ぶ）。 偏角 $\theta$ が、指数の肩に乗ってくる。

$z = x + iy$ を使って、複素指数関数にオイラーの公式を適用しよう。 $e^{z+w} = e^z e^w$ という基本指数法則が成り立つことは先に確認したので、 \begin{align*} e^z = e^{x+ iy} = e^x e^{iy} = e^x(\cos(y) + i\sin(y)) \end{align*} という関係になる。 $e^z = e^{x+iy}$ の絶対値は $e^x \;(\gt 0)$ であり、偏角は $y$ になるのである。

また $k \in \mathbb{Z}$ とすると、 $\displaystyle{ e^{i \cdot 2k\pi} = \cos(2k\pi) + i\sin(2k\pi) = 1 }$ であるから \begin{align*} e^{z + i\cdot 2k\pi} = e^z e^{i \cdot 2k\pi} = e^z \end{align*} という結果が得られる。 これは、$e^z$ が周期 $i \cdot 2k\pi$ を持つ周期関数であることを意味している。 この結果から \begin{align*} e^z = e^{z + i\cdot 2k\pi} = e^{x+ iy + i\cdot 2k\pi} = e^x e^{i\cdot (y + 2k\pi)} \end{align*} となり、$e^z = e^{x+iy}$ については $y + 2k\pi$ も偏角であることがわかる。 $e^z$ の内部自由度がこのようにして炙り出されてくる。 次の図は、理解の助けになるかもしれない：

$\square$ 複素関数の捉え方

１変数関数 $y = f(x)$ は、数 $x$ と数 $y$ の対応であり、それをうまく可視化したものが $x$-$y$ 平面上のグラフである、といって良いと思う。 いっぽうで複素関数 $w = f(z)$ は、$z$ の素性が $z = x + iy$ であることからあきらかなように、独立変数が２個ある関数であり、従属変数も複素数であることから２個存在する。 この関係をどのように可視化（またはイメージ化）すればよいだろうか？ ２次元から２次元ということを踏まえて、２つの平面どうしの対応と捉えるのが素直だと思われる。 そこで、混乱を起こさないように、独立変数が存在する２次元を $x$-$y$ 平面、そしてその像となる従属変数が存在する２次元を $u$-$v$ 平面と呼び分けるのが学習の知恵であるような気がする。 もちろんその２つの平面はともに複素平面である。

つまり、複素関数 $w = f(z)$ において、 $z = x+ iy$、$w = u + iv$ と考えて、関数の働きを \begin{align*} f: z \longmapsto w \iff f: (x, y) \longmapsto (u, v) \end{align*} ととらえるのが良いのではないかと思っている。 これを元にして

複素関数 $f$ というものは、複素平面$(x,y)$ から複素平面$(u,v)$ への変換（写像）であるとイメージする

のが賢明なのではないだろうか。 そしてそのときには、$u,\, v$ ともに $(x, y)$ の関数であるという見立てになる（すなわち $u = u(x, y),\, v = v(x, y)$）。 上の複素指数関数の対応図は、こういう意図の元で記したものである。 その図からあきらかなように \begin{alignat*}{2} & u = e^x\cos(y),& &\quad v = e^x\sin(y) \\ & u = e^x\cos(y+2\pi),& &\quad v = e^x\sin(y+2\pi) \\ & \cdots & &\quad\cdots \end{alignat*} という関係になっている。

$\square$ １価関数であることの確認

さて、この複素指数関数は１価関数であるか、と問うてみる。 １価関数である事は上の図からもほぼあきらかであるけれど、そもそもの複素指数関数の定義に戻って確認してみよう。

$z$ を決めると $z^2,\, z^3,\, \ldots,\, z^n$ はユニークに決まるということは素直に諒解できると思う。 実際 $z$ の持つ内部自由度をおもてに出す表現 $z = re^{i\theta} = re^{i\cdot (\theta + 2k\pi)}$ を使っても、 \begin{align*} z^n = \left(re^{i\theta}\right)^n = \overbrace{re^{i\theta} \cdot re^{i\theta} \cdots re^{i\theta}}^{n\;\text{個}} = r^n e^{i\cdot n\theta} \end{align*} であるし、$e^{i\cdot (\theta + 2k\pi)} = e^{i\theta}e^{i\cdot 2k\pi} = e^{i\theta}$ を利用すれば \begin{align*} z^n = \left(re^{i\cdot (\theta + 2k\pi)}\right)^n = \left(re^{i\theta}e^{i\cdot 2k\pi}\right)^n = \left(r^ne^{i\cdot n\theta}\right)\left(e^{i\cdot 2nk\pi}\right) = r^n e^{i\cdot n\theta} \end{align*} となるので、 $z^n$ について偏角の不定性がおもてに現れることはない。 つまり $z$ の内部自由度は出てこない。 その諒解のもとで、指数関数 $\displaystyle{f(z) = e^z = \sum_{n=0}^\infty \frac{z^n}{n!}}$ を見直せば、この関数が１価関数であることは火を見るよりも‥‥と言って良いだろう。

付け加えれば、複素数の四則演算の結果は複素数になるので（$z = x+ iy,\, \alpha = a+ib,\, \beta = c + id$ として $\alpha z + \beta = p + iq$ となることは簡単な計算により示すことができよう）、$e^{\alpha z + \beta}$ も１価関数である。

複素指数関数の導入によって極形式の表現方法の重要度が高まってきた。 そこで、偏角というものの不定性にまつわる性質も少し吟味しておかねばならぬ。 それゆえに、次の節でまた脇道に逸れて、$\arg$ という偏角関数（多価関数）について考察してみたいと思う。

---

$\arg(z)$ という偏角関数

$\square$ $\arg(z)$ の表現

$z$ を極形式であらわしたときの $\theta$、すなわち $z = r(\cos\theta + i\sin\theta) = re^{i\cdot \theta}$ の $\theta$ を偏角と呼ぶことは先に述べた（本稿では特別に、$0 \le \theta \lt 2\pi$ という条件をつけておいた）。 そしてこの偏角には不定性があることも申し上げた。 ここで、$z$ の偏角を導く関数を $\arg(z)$ と書くことにしよう。 偏角には不定性があった。 それゆえ一つの $z$ に対し複数の偏角が存在する。 したがって $\arg(z)$ は多価関数となるのである。 そして、複素平面と極形式の形から \begin{align*} \arg(z) = \arg(re^{i\theta}) = \theta + 2k\pi \quad(k \in \mathbb{Z}) \end{align*} であることが見通せる。 この $\arg(z)$ を、数の集合として考えるならば（そして １価関数と多価関数 で採用した表現方法を用いれば） \begin{align*} \arg(z) = \set{\theta + 2k\pi \mid k \in \mathbb{Z}} = \theta + \set{2k\pi \mid k \in \mathbb{Z}} \end{align*} というようにも表現できる。

$\square$ 重要な性質

この偏角関数 $\arg$ には \begin{align*} \arg(zw) = \arg(z) + \arg(w) \end{align*} という、ある意味で、というか、複素対数関数を考えるときに役に立つというか、とにかく重要な関係が存在している。 対数関数でおなじみの「積が和になる」という形式だ。 $z = re^{i\theta},\, w = r^\prime e^{i\theta^\prime}$ とすると \begin{align*} zw = re^{i\theta} \cdot r^\prime e^{i\theta^\prime} = rr^\prime e^{i\theta}e^{i\theta^\prime} = rr^\prime e^{i\cdot (\theta + \theta^\prime)} \end{align*} であるから \begin{align*} \arg(zw) = \arg\left(rr^\prime e^{i\cdot (\theta + \theta^\prime)}\right) = (\theta + \theta^\prime) + 2k\pi \end{align*} となる。 一方 \begin{align*} & \arg(z) = \theta + 2l\pi \;, \\ & \arg(w) = \theta^\prime + 2l^\prime\pi \end{align*} であるから \begin{align*} \arg(z) + \arg(w) = \theta + 2l\pi + \theta^\prime + 2l^\prime\pi = \theta + \theta^\prime + 2(l + l^\prime)\pi \end{align*} となる。 ここで $l + l^\prime$ の実態は、まず $l$ を固定すると $l + 0, l \pm 1, l \pm 2, \ldots$ であり、その上で $l$ が整数全体に広がるのであるから、整数全体をカバーしておりまた整数全体からはみ出るものもない（無限集合を扱う際の定番の考え方だ）。 したがって $k = l + l^\prime$ とあらわすことができ、結果 $\arg(z) + \arg(w) = \theta + \theta^\prime + 2k\pi$ となって、$\arg(zw)$ と等しいことになる。

同様にして、「割り算が引き算になる」という関係も存在する。 これも対数関数でおなじみの事柄だ。 \begin{align*} \arg\left(\frac{z}{w}\right) = \arg\left(\frac{r}{r^\prime}\frac{e^{i\cdot\theta}}{e^{i\cdot\theta^\prime}}\right) = \arg\left(\frac{r}{r^\prime}e^{i\cdot(\theta - \theta^\prime)}\right) = \theta - \theta^\prime + 2k\pi \end{align*} であり、また \begin{align*} \arg(z) - \arg(w) = (\theta + 2l\pi) - (\theta^\prime + 2l^\prime\pi) = \theta - \theta^\prime + 2(l - l^\prime)\pi \end{align*} である。先と同じ論法で $ \set{2k\pi \mid k \in \mathbb{Z}} = \set{2(l - l^\prime)\pi \mid l,\, l^\prime \in \mathbb{Z}} $ がいえるので \begin{align*} \arg\left(\frac{z}{w}\right) = \arg(z) - \arg(w) \;. \end{align*}

$\bullet$ 実数の偏角とのコンビネーション

絶対値と偏角 のところでみたように、一般の実数 $p$ についてその偏角は \begin{align*} \arg(p) = \begin{cases} 2k\pi &\quad(p \gt 0) \\ \pi + 2k\pi &\quad(p \lt 0) \end{cases} \quad(p \in \mathbb{R}, k \in \mathbb{Z}) \end{align*} と $\arg$ 関数を使って表現することができる。 そして、$\arg(z)$ には $2k\pi$ の不定性が繰り込まれているので、 \begin{align*} \arg(pz) = \arg(p) + \arg(z) = \begin{cases} 2k\pi + \arg(z) = \arg(z) &\quad(p \gt 0) \\ \pi + 2k\pi + \arg(z) = \pi + \arg(z) &\quad(p \lt 0) \\ \end{cases} \end{align*} という変形が可能となる。 同じように、 \begin{align*} \arg\left(\frac{p}{z}\right) = \arg(p) - \arg(z) = \begin{cases} 2k\pi - \arg(z) = -\arg(z) &\quad(p \gt 0) \\ \pi + 2k\pi - \arg(z) = \pi - \arg(z) &\quad(p \lt 0) \\ \end{cases} \end{align*} となる。 これより、$p = 1$ のときには \begin{align*} \arg\left(\frac{1}{z}\right) = \arg(1) - \arg(z) = -\arg(z) \end{align*} となる。 この結果は、複素指数関数を利用することだけでも導き出せる。 $z = re^{i\theta}$ とすると $1/z = (1/r)e^{-i\theta}$ であるから \begin{align*} \arg\left(\frac{1}{z}\right) = \arg\left(\frac{1}{r}e^{-i\theta}\right) = -\theta + 2k\pi = -(\theta + 2k^\prime\pi) = - \arg(z) \quad(k, k^\prime \in \mathbb{Z})\;. \end{align*}

$\square$ 厄介な性質

ところが、厄介なことに \begin{align*} \arg(z) + \arg(z) \neq 2\arg(z) \end{align*} なのである。 少なからず意外な事柄である。 なぜか？ まず先の結果を利用して \begin{align*} \arg(z) + \arg(z) = 2\theta + 2k\pi = 2\theta + \set{2k\pi \mid k \in \mathbb{Z}} \end{align*} となることは良いであろう。 しかしながら \begin{align*} 2\arg(z) = 2(\theta + 2l\pi) = 2\theta + 4l\pi = 2\theta + \set{4l\pi \mid l \in \mathbb{Z}} \end{align*} である。 このとき集合どうしを比較すれば \begin{align*} \set{4l\pi \mid l \in \mathbb{Z}} \subsetneq \set{2k\pi \mid k \in \mathbb{Z}} \end{align*} となって、部分集合ではあるが、等しくは、ない。 それゆえ、 \begin{align*} \arg(z^2) = \arg(zz) = \arg(z) + \arg(z) \neq 2\arg(z) \end{align*} なのである。

$\arg(z/z) = \arg(z) - \arg(z)$ についても厄介さはおなじで、 \begin{align*} \arg(z) - \arg(z) = 2k\pi \neq 0 \end{align*} なのである。 この結果はまた $\arg(z/z) = \arg(1) = 2k\pi$ という実数の偏角の不定性の事実も裏付けている。

$\square$ 再び複素数の新たな表記法

さて気を取り直して。 $\arg$ 関数を導入することにより、$z$ の偏角は $\arg(z)$ と $z$ 自身であらわすことができるようになった。 また絶対値も $\abs{z}$ と $z$ 自身であらわせる。 したがって、$z$ を、他のパラメタを介さずに \begin{align*} z = re^{i\cdot \theta} = \abs{z}e^{i\cdot \arg(z)} \end{align*} と自分自身で表現する形式も得られるのである。 さらにまたこの記述では、指数の肩に多価関数の $\arg(z)$ が乗っていることからわかるように、偏角の不定性が内在されている。 つまり $z$ の内部自由度が表面にあらわれてきているのである。 さらに付け加えれば、この $\arg(z)$ こそが、これから見てゆく複素対数関数や一般の複素指数関数、複素冪乗関数に多価性をもたらすのである。 繰り返しになるが、その内部自由度は $\arg(z)$ の中にある。

---

複素対数関数

$\square$ 定義と構築

複素数の指数関数を手に入れたので、それの逆関係を考えていこう。 $z = f(w) = e^w$ であるときに $w$ を求めることができる $z$ の関数はどのようなもか、ということである。 実数までの世界の類推で、まず \begin{align*} w = \mathbb{log}_e{z} \end{align*} という記法を援用しよう。 指数関数の逆には対数関数という名前が付くのが習わしであるので、これを複素対数関数と呼ぶことにする。 忘れてはならないことは、この複素対数関数の背中には常に $z = e^w$ という関係が横たわっているということである。 指数関数なしでは対数関数は導けない （とは言っても、数学の発展史においては、指数よりも先に対数関数が見出されていたらしい^[3]。 先人達の偉大さに改めて感動する）。

実関数の場合には、$y = e^x \;\;(-\infty \lt x \lt \infty)$ としたとき、$x$ と $y$ の間には１対１の対応があるので、逆関数つまり対数関数の存在については疑いがない。かつ、$y \gt 0$ となるので、対数関数は $x = \log_e{y} \;\;(y \gt 0)$ となる（実関数のときには、独立変数 $y$ の定義域が制限されてくるところが興味深い。これが「対数の真数は正」というスローガンにつながる）。 しからば複素対数関数の場合はどうであろうか。

前にもみたように、複素数指数関数には周期性があり、それは \begin{align*} z = e^w = e^{w + i\cdot 2\pi} = e^{w - i\cdot 2\pi} = \cdots = e^{w + i\cdot 2k\pi} \quad(k \in \mathbb{Z}) \end{align*} というようにあらわせるのであった。 それゆえ $w = \mathbb{log}_e{z}$ であるならば、$w + i\cdot 2\pi$ にも同じ権利があっても良いはずである。 $w - i\cdot 2\pi$ や $w + i\cdot 4\pi$ などについても同様。 それらの権利を保証してまとめて書いてみると \begin{align} \begin{aligned} w &= \mathbb{log}_e{z} \\ w + i\cdot 2\pi &= \mathbb{log}_e{z} \\ w - i\cdot 2\pi &= \mathbb{log}_e{z} \\ &\cdots \\ w + i\cdot 2k\pi &= \mathbb{log}_e{z} \end{aligned} \label{eq.log.01} \end{align} となる。 ここまで来たら、そして本稿全体の流れから容易に察せられるように、複素対数関数 $\mathbb{log}_e{z}$ は、その定義から、生まれつき多価関数（無限個の値を持つ）になっているのである。

複素対数関数は多価関数であるという事情をもう少し整理してみよう。 $z$ は $z = \abs{z}e^{i\cdot \arg(z)}$ とあらわせた。 $\abs{z}$ は実数であるから、実対数関数を使って $\abs{z} = e^{\log_e{\abs{z}}}$ とあらわせる（$a = e^{\log_e{a}}$ という指数と対数の１回ひねり的帰結）。 それゆえ \begin{align*} z = \abs{z}e^{i\cdot \arg(z)} = e^{\log_e{\abs{z}}}e^{i\cdot \arg(z)} = e^{\log_e{\abs{z}} + i\cdot \arg(z)} \;. \end{align*} ここであらためて $w = \log_e{\abs{z}} + i\cdot \arg(z)$ とおけば、この式は $z = e^w$ に他ならないから \begin{align*} w = \mathbb{log}_e{z} \quad\therefore\;\; \mathbb{log}_e{z} = \log_e{\abs{z}} + i\cdot \arg(z) \end{align*} という、$z$ 自身による複素対数関数 $\mathbb{log}_e{z}$ の表現が得られるのである。 そしてこの表現式からあきらかなように、複素対数関数の多価性は、変数である $z$ の偏角 $\arg(z)$ の多価性に起因している。 $z$ の内部自由度が、複素対数関数においても、おもてに現れてくるのである。

$\arg(z)$ は、$\arg(z) = \theta + 2k\pi$ とほどくことができるので、$k$ の値に応じて \begin{alignat*}{2} w_0 &= \log_e{\abs{z}} + i\cdot \theta & &\qquad(k = 0) \\ w_1 &= \log_e{\abs{z}} + i\cdot (\theta + 2\pi) & &\qquad(k = 1) \\ w_{-1} &= \log_e{\abs{z}} + i\cdot (\theta - 2\pi) & &\qquad(k = -1) \\ w_2 &= \log_e{\abs{z}} + i\cdot (\theta + 4\pi) & &\qquad(k = 2) \\ w_{-2} &= \log_e{\abs{z}} + i\cdot (\theta - 4\pi) & &\qquad(k = -2) \\ & \cdots\cdots \end{alignat*} と表記すれば、この多価関数性は次のように図示できる（先に見た複素指数関数の図と良い対照をなしている）：

この無限個の対応をまとめてあらわしたものが $\mathbb{log}_e{z} = \log_e{\abs{z}} + i\cdot \arg(z)$ に他ならない。 \eqref{eq.log.01} でみた「保証」がきちんと成立していることもあきらかである。

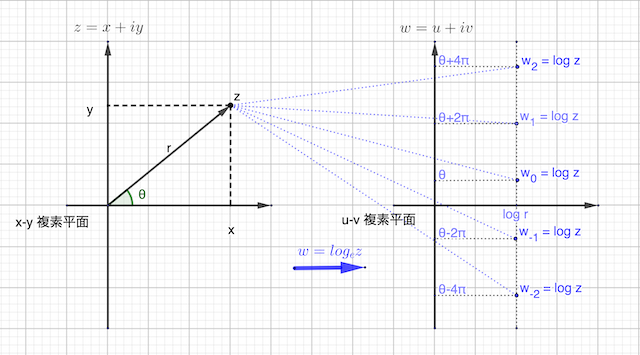
$\mathbb{log}_e{z} = \log_e{\abs{z}} + i\cdot \arg(z)$ という結果から対数関数らしい性質が導出できる。 任意の複素数 $\eta,\, \mu$ において \begin{align*} \mathbb{log}_e{\eta} &= \log_e{\abs{\eta}} + i\cdot\arg(\eta) \;, \\ \mathbb{log}_e{\mu} &= \log_e{\abs{\mu}} + i\cdot\arg(\mu) \end{align*} より \begin{align*} \mathbb{log}_e{\eta} + \mathbb{log}_e{\mu} &= \log_e{\abs{\eta}} + \log_e{\abs{\mu}} + i\cdot\arg(\eta) + i\cdot\arg(\mu) \\ &= \log_e{\abs{\eta}} + \log_e{\abs{\mu}} + i\cdot\left(\arg(\eta) + \arg(\mu)\right) \end{align*} となる。 絶対値に関わっている対数は実対数関数であることから $\log_e{\abs{\eta}} + \log_e{\abs{\mu}} = \log_e{\abs{\eta\mu}}$ であり、偏角関数 $\arg$ の「積と和の関係」を利用すると \begin{align*} \mathbb{log}_e{\eta} + \mathbb{log}_e{\mu} = \log_e{\abs{\eta\mu}} + i\cdot\arg(\eta\mu) = \mathbb{log}_e{\eta\mu} \;. \end{align*}

同様にして \begin{align*} \mathbb{log}_e{\eta} - \mathbb{log}_e{\mu} &= \log_e{\abs{\eta}} - \log_e{\abs{\mu}} + i\cdot\arg(\eta) - i\cdot\arg(\mu) \\ &= \log_e{\abs{\frac{\eta}{\mu}}} + i\cdot\left(\arg(\eta) - \arg(\mu)\right) \end{align*} であり、$\arg$ の「割り算が引き算になる」関係を使って \begin{align*} \mathbb{log}_e{\eta} - \mathbb{log}_e{\mu} = \log_e{\abs{\frac{\eta}{\mu}}} + i\cdot\arg\left(\frac{\eta}{\mu}\right) = \mathbb{log}_e{\frac{\eta}{\mu}} \;. \end{align*}

$\square$ $e^{\mathbb{log}_e{z}}$ という関数

$\mathbb{log}_e{z}$ は多価関数であるけれども、それが複素指数関数の肩に乗った場合は１価関数になる、という事実を示しておこう。 計算を実行すれば \begin{align*} e^{\mathbb{log}_e{z}} = e^{\log_e{\abs{z}} + i\cdot\arg(z)} = e^{\log_e{\abs{z}} + i(\theta + 2l\pi)} = e^{\log_e{\abs{z}} + i\theta} e^{i\cdot 2l\pi} = e^{\log_e{\abs{z}} + i\theta} \end{align*} となって、不定性はすべて $e^{i\cdot 2l\pi} = 1$ に吸収されてしまう。 したがって１価関数。

しかしながら、$e^{\alpha \,\mathbb{log}_e{z}}$ は \begin{align*} e^{\alpha\,\mathbb{log}_e{z}} = e^{\alpha(\log_e{\abs{z}} + i\cdot\arg(z))} = e^{\alpha\log_e{\abs{z}} + i\cdot\alpha\arg(z)} = e^{\alpha\log_e{\abs{z}} + i\cdot\alpha(\theta + 2l\pi)} = e^{\alpha\log_e{\abs{z}} + i\alpha\theta} e^{i\cdot \alpha \cdot 2l\pi} \end{align*} となり、一般には $e^{i\cdot \alpha \cdot 2l\pi}$ が残る。 $\alpha = k \;\; (k \in \mathbb{Z})$ であれば、$e^{i\cdot k \cdot 2l\pi} = 1$ となり不定性が吸収されて、１価関数となる。

$\square$ 意表をつかれる事柄

うっかりすると危うい、そして実数までの世界に慣れた身体には意外な事実を、この節の最後に記そう。

冒頭では $z = e^w$ をもとにして \begin{align*} \mathbb{log}_e{z} = w + i\cdot 2k\pi \end{align*} を導いた。 ここで $z$ をそもそもの形 $e^w$ に置き換えると \begin{align*} \mathbb{log}_e{e^w} = w + i\cdot 2k\pi \end{align*} となる。 実数のときの関係 $\log{e^x} = x$ とは大違いなのである。 多価関数の多価関数たる所以でもある。 なお、この計算は次のようにしても確認できる（途中で $w = x + iy$ としている）： \begin{align*} \mathbb{log}_e{e^w} &= \log_e\abs{e^w} + i\cdot \arg(e^w) = \log_e\abs{e^{x + iy}} + i\cdot \arg(e^{x+iy}) \\ &= \log_e{e^x} + i\cdot (y + 2k\pi) = x + iy + i\cdot 2k\pi \\ &= w + i\cdot 2k\pi \;. \end{align*}

$\mathbb{log}_e{z^2} \neq 2\,\mathbb{log}_e{z}$ というこれまた意外な結果も導出される。 $\mathbb{log}_e{zw} = \mathbb{log}_e{z} + \mathbb{log}_e{w}$ であるから、 \begin{align*} \mathbb{log}_e{z^2} = \mathbb{log}_e{zz} &= \mathbb{log}_e{z} + \mathbb{log}_e{z} \\ &= \log_e\abs{z} + i\cdot\arg(z) + \log_e\abs{z} + i\cdot\arg(z) \\ &= 2\log_e\abs{z} + i\cdot\left(\arg(z) + \arg(z)\right) \;. \end{align*} しかしながら \begin{align*} 2\,\mathbb{log}_e{z} &= 2\log_e\abs{z} + i\cdot2\arg(z) \end{align*} であり、$2\arg(z) \neq \arg(z) + \arg(z)$ であったから （$arg(z)$ という偏角関数を参照）、結果 \begin{align*} \mathbb{log}_e{z^2} = \mathbb{log}_e{z} + \mathbb{log}_e{z} \neq 2\,\mathbb{log}_e{z} \end{align*} となるのである。 $2$ を聞いて $n$ を知る、という格言に従えば、この結果から自ずと \begin{align*} \mathbb{log}_e{z^n} \neq n\,\mathbb{log}_e{z} \end{align*} となるのである。

---

複素指数関数の一般化と複素冪乗関数

$\square$ 定義と構築

一般の複素指数関数 $w = f(z)$ と、複素冪乗関数 $w = g(z)$ は \begin{align*} & f(z) = \alpha^z = e^{z\,\mathbb{log}_e{\alpha}} \\ & g(z) = z^\beta = e^{\beta\,\mathbb{log}_e{z}} \end{align*} と定義される。 そのまま素直純心にこの定義を受け入れて、先に進むという道がある。 しかしながら、そこに何がしかの理由はないのだろうか、と悩みたい。

定義というものを個人的に分類してみると、どうも２つのタイプに分かれるように思える。 ひとつは、その言葉の意味を決めるようなもの（例えば「一様収束」の定義。そう、あの $\varepsilon$-$\delta$ 論法なしでは理解できない悪名高い（？）やつ）、数式の記法を定めるもの（例えば $f^{(n)} = d^nf/dx^n$ など）などである。このタイプのものは「定義」という語感にしっくりくる。 もうひとつは「このように仮定すると、今までの経験から全てが万事矛盾なくうまくいく（のではあるまいか）、こう決めると面白いことになる、こうするといろいろ辻褄があって新しい世界が見えてくる」という類の定義である。 物理の世界ではこのタイプのものには「仮説」という言葉が使われることが多いような気がするけれど、数学の世界だと「定義」というものにその仮説的なニュアンスが込められているような気がする。 そしてかそれゆえか、しっくり感が薄い。 言葉悪いけど、騙されている感が拭えない。 なので、何らかの裏付けが欲しくなる時があるのである。

上で持ち込んだ定義は、実数関数からの「演繹」である。 演繹というのが相応しくなければ、拡張と言っても良い。 とにかく、実関数世界での裏付けがあるものであるから、信用して良い定義である。 それを踏まえて、ここでもこの定義のもっともらしさを記してみることにする。

$f(z) = e^{\gamma z} \;\;(\gamma \in \mathbb{C})$ という関数を考える。 基本指数法則から \begin{align*} f(z + w) = e^{\gamma (z+w)} = e^{\gamma z}e^{\gamma w} = f(z)f(w) \end{align*} が導けて、この論法を使うと \begin{align*} f(z_1 + z_2 + \cdots + z_n) = f(z_1)f(z_2) \cdots f(z_n) \end{align*} となる。 ここで $z_i = 1 \;\;(\text{for all } i)$ と実験する。 その際 $f(1) = e^\gamma =: \mu$ であるとしておくと、 \begin{align*} f(n) = (f(1))^n = \mu^n \end{align*} となる。 一方で $\mu$ の取り決めから $e^\gamma = \mu \iff \gamma = \mathbb{log}_e{\mu}$ であるので \begin{align*} f(n) = \mu^n = \left(e^\gamma\right)^n = e^{n\gamma} = e^{n\,\mathbb{log}_e{\mu}} \quad \text{（$n$ は自然数なので肩から降りる）} \end{align*} となる。 そしてここで、ある飛躍をするのである。 自然数 $n$ に対して成り立つこの式を、思い切って複素数でも成り立つだろうと考えるのである。すると \begin{align*} f(z) = \mu^z = e^{z\,\mathbb{log}_e{\mu}} \;. \end{align*} また、$z$ と $\mu$ を入れ替えれば \begin{align*} z^\mu = e^{\mu\,\mathbb{log}_e{z}} \;. \end{align*} 以上の結果から、定義が何となくそれらしく思えてくるではなかろうか^[4]。

$\square$ 多価性の要因の違い

さて、定義についてそれなりの確信が持てたので、この両者の関数の特徴を少し探ってみよう。 ここまでみてきたように、一般の複素指数関数と複素冪乗関数は形式は全く同じである。 区別する点は、何を変数とみるか、である。 変数を $z$ として \begin{align} \begin{aligned} \text{一般の複素指数関数} &\;:\; f(z) = \alpha^z = e^{z\,\mathbb{log}_e{\alpha}} \\ \text{複素冪乗関数} &\;:\; g(z) = z^\beta = e^{\beta\,\mathbb{log}_e{z}} \end{aligned} \label{eq.power.01} \end{align} と命名する。 両者は形式は同じなので、代数的操作はどちらについても変わらない。 それゆえ、変数というものをいったん忘れて式変形に向かおう。 変数を忘れるために $\alpha^\beta$ という形式で考えると \begin{align*} \alpha^\beta = e^{\beta \,\mathbb{log}_e{\alpha}} = e^{\beta (\log_e{\abs{\alpha}} + i\cdot\arg(\alpha))} = e^{\beta \log_e{\abs{\alpha}}} e^{i\cdot\beta\cdot\arg(\alpha)} \end{align*} となる。 $\log_e{\abs{\alpha}}$ は実数であるから、$e^{\beta\log_e{\abs{\alpha}}}$ は１意に定まり不定性はない。 したがって、$\alpha^\beta$ の不定性は、$\arg(\alpha)$ の不定性、すなわち $\alpha$ の内部自由度によってもたらされることがわかる。

この結果を一般の複素指数関数に適用するには、$\beta = z$ とすればよい。 その上で式変形を少し巻き戻せば \begin{align} \begin{aligned} \alpha^z = e^{z \left(\log_e{\abs{\alpha}} + i\cdot\arg(\alpha)\right)} &= \begin{cases} e^{z \left(\log_e{\abs{\alpha}} + i\theta\right)} \\ e^{z \left(\log_e{\abs{\alpha}} + i(\theta \pm 2\pi)\right)} \\ e^{z \left(\log_e{\abs{\alpha}} + i(\theta \pm 4\pi)\right)} \\ \cdots\cdots \end{cases} \\ &= \set{\left. e^{z \left(\log_e{\abs{\alpha}} + i(\theta + 2k\pi)\right)} \;\right|\; k \in \mathbb{Z}} \end{aligned} \label{eq.power.02} \end{align} というようになる。 つまりたくさんの複素指数関数（そして１価関数）の集合になるのである（複素指数関数が１価関数であることは複素指数関数と複素三角関数で考察した）。 そしてそれは、$\alpha$ の内部自由度による不定性からもたらされる「多価関数化」なのである。

一方で、複素冪乗関数では、$\alpha = z$ とすればよく、 \begin{align} \begin{aligned} z^\beta = e^{\beta \left(\log_e{\abs{z}} + i\cdot\arg(z)\right)} &= \begin{cases} e^{\beta \left(\log_e{\abs{z}} + i\theta\right)} \\ e^{\beta \left(\log_e{\abs{z}} + i(\theta \pm 2\pi)\right)} \\ e^{\beta \left(\log_e{\abs{z}} + i(\theta \pm 4\pi)\right)} \\ \cdots\cdots \end{cases} \\ &= \set{\left. e^{\beta \left(\log_e{\abs{z}} + i(\theta + 2k\pi)\right)} \;\right|\; k \in \mathbb{Z}} \\ \end{aligned} \label{eq.power.03} \end{align} となる。 これは、$z$ を固定しても関数値が異なるという通常の多価関数である。 多価関数化は、$\arg(z)$ の多価性すなわち $z$ の内部自由度による不定性からもたらされる。

つまり、一般の複素指数関数と複素冪乗関数では、多価関数の形態とそれがもたらされる原因が異なっているのである。

$\square$ 複素対数関数への適用

次に複素対数をとるとどうなるか、に注目してみよう。 先と同様に $\alpha^\beta$ から考えるのだけれど、途中で $\beta = c + id$ という置き換えを挟んで実行する。 少しばかり長い計算になる。 出発点は \begin{align*} \alpha^\beta = e^{\beta \,\mathbb{log}_e{\alpha}} = e^{\beta (\log_e{\abs{\alpha}} + i\cdot\arg(\alpha))} = e^{(c + id)(\log_e{\abs{\alpha}} + i\cdot\arg(\alpha))} \end{align*} であり、このとき \begin{align*} (c + id)(\log_e{\abs{\alpha}} + i\cdot\arg(\alpha)) &= c\log_e{\abs{\alpha}} + i\cdot c \cdot \arg(\alpha) + i\cdot d\log_e{\abs{\alpha}} - d\cdot\arg(\alpha) \\ &= c\log_e{\abs{\alpha}} - d\cdot\arg(\alpha) + i(c \cdot \arg(\alpha) + d\log_e{\abs{\alpha}}) \\ &=: p + iq \\ &\left(p = c\log_e{\abs{\alpha}} - d\cdot\arg(\alpha),\;\; q = c \cdot \arg(\alpha) + d\log_e{\abs{\alpha}}\right) \end{align*} と計算できるので、結局のところ \begin{align*} & \alpha^\beta = e^{p + iq} = e^p e^{iq} \\ &\therefore\;\; \abs{\alpha^\beta} = e^p \;, \quad \arg\left(\alpha^\beta\right) = q + 2k\pi \;. \end{align*} それゆえ \begin{align*} \mathbb{log}_e{\alpha^\beta} = \log_e{\abs{\alpha^\beta}} + i\cdot\arg\left(\alpha^\beta\right) = \log_e{e^p} + i(q + 2k\pi) \end{align*} ここで $p,\, q$ をほどく。 $\log_e{e^p}$ は実対数関数であるから \begin{align*} & \log_e{e^p} = p = c\log_e{\abs{\alpha}} - d\cdot\arg(\alpha) \;, \\ & q + 2k\pi = c \cdot \arg(\alpha) + d\log_e{\abs{\alpha}} + 2k\pi \;. \end{align*} したがって \begin{align*} \mathbb{log}_e{\alpha^\beta} &= \log_e{e^p} + i(q + 2k\pi) \\ &= c\log_e{\abs{\alpha}} - d\cdot\arg(\alpha) + i(c \cdot \arg(\alpha) + d\log_e{\abs{\alpha}} + 2k\pi) \\ &= (c + id)\log_e{\abs{\alpha}} + i\cdot((c +id)\arg(\alpha)) + i\cdot 2k\pi \\ &= (c + id)\left(\log_e{\abs{\alpha}} + i\cdot\arg(\alpha)\right) + i\cdot 2k\pi \\ &= (c + id)\,\mathbb{log}_e{\alpha} + i\cdot 2k\pi \\ &= \beta\,\mathbb{log}_e{\alpha} + i\cdot 2k\pi \end{align*} となる。 それゆえ、一般の複素指数関数は $\beta = z$、複素冪乗関数は $\alpha = z$ とすれば良いので、 \begin{align*} & \mathbb{log}_e{\alpha^z} = z\,\mathbb{log}_e{\alpha} + i\cdot 2k\pi \\ & \mathbb{log}_e{z^\beta} = \beta\,\mathbb{log}_e{z} + i\cdot 2k\pi \end{align*} という結果を得るのである。

と、だらだら計算してきたが、そもそも \eqref{eq.power.02}、\eqref{eq.power.03} 、いやもっと遡れば \eqref{eq.power.01} と複素対数関数の定義から、この結果はあきらかではないか、とほほ。

$\square$ ネイピア数の指数乗

一般の複素指数関数において、その底をネイピア数にしてみよう。 混乱を起こさないように、ネイピア数を $E = 2.718\cdots$ とする。 また実数の世界での事実 $\log_e{E} = 1$ を援用する。

$E^z$ については、今さっき見てきたように、複素指数関数を用いて \begin{align*} E^z = e^{z\,\mathbb{log}_e{E}} = e^{z(\log_e{\abs{E}} + i\cdot\arg(E))} \end{align*} となる。 そして $E$ は正の実数であるから、 \begin{align*} \log_e{\abs{E}} = \log_e{E} = 1 \;, \quad \arg(E) = \set{2k\pi \mid k \in \mathbb{Z}} \;. \end{align*} とくに偏角として $0 \in \arg(E)$ を選ぶと \begin{align*} \left. E^z \right|_{arg = 0} = e^{z\log_e{\abs{E}}} = e^z \end{align*} となる（左辺は、$0$ を偏角として選んだ事を示したいためにあつらえた記法）。 つまり、複素指数関数 $e^z$ とは、$E^z$ で求められる無限個の関数のうち、もっともシンプルなものを選んだものである、ということもできるのである。 けれども、$e^z$ の定義がなければ $\mathbb{log}_e{E}$ も $E^z$ も求められなかったのだから、これはあくまでも結果をみての解釈なのだ。 始めに $E^z$ があるわけではない。 ま、これによって、$e^z$ がネイピア数の $z$ 乗と同じ値をもつ（ただし $\arg(E) = 0$ の場合）という通常的な結論が得られたことも確かなのではある。

---

主値

$\square$ 主値という考え方

場合によっては、たくさんの偏角を考えることが不要な時もある。 $\arg(z) = \theta + 2k\pi$ という関係は、偏角の範囲に何も制限をつけなかったので、$2\pi$ ごとに周期が繰り返されて、複数の値を持つという事態になっていた。 そこで \begin{align*} 0 \leq \theta \lt 2\pi \quad\text{とか}\quad -\pi \lt \theta \leq \pi \end{align*} などのような１周期分の制限を付け（この制限を「主値条件」と名付ける）、その制限の中にあるものを取り出すと言う操作を考える。

このようにして取り出されたひとつの偏角を $Arg(z)$ と書いて、「偏角 $\arg(z)$ の主値」と呼んでいる。 代表値という言葉の方が実態に近い気がするが、ま、それはおいておこう。 もちろん $Arg(z)$ これは１価関数である。 $\arg(z)$ との関係は、主値条件として $0 \leq \theta \lt 2\pi$ を採用すると \begin{align*} Arg(z) \in \arg(z) \;, \quad 0 \leq Arg(z) \lt 2\pi \end{align*} であり、 \begin{align*} \arg(z) = Arg(z) + 2k\pi \quad(k \in \mathbb{Z}) \quad\text{または}\quad \arg(z) = \set{Arg(z) + 2k\pi \mid k \in \mathbb{Z}} \end{align*} ということになる。

偏角の主値 $Arg(z)$ を用いて、複素対数関数を１価関数にしたものもを $\mathbb{Log}_e$ と書く。 複素対数関数の主値とも言われる。 $\mathbb{Log}_e$ は \begin{align*} \mathbb{log}_e{z} = \log_e{\abs{z}} + i\cdot \arg(z) = \log_e{\abs{z}} + i\cdot Arg(z) + i\cdot 2k\pi \end{align*} から不定部分を除いたもの（１価関数化）、すなわち \begin{align*} \mathbb{Log}_e{z} = \log_e{\abs{z}} + i\cdot Arg(z) \end{align*} である。

複素冪乗関数 $w = z^\beta = e^{\beta\mathbb{log}_e{z}}$ に対しても、$\mathbb{log}_e$ を $\mathbb{Log}_e$ にすること、つまり \begin{align*} w = z^\beta = e^{\beta\mathbb{Log}_e{z}} \end{align*} とすることで、１価関数化ができる。 これは複素冪乗関数の主値と言われる。 一般の複素指数関数も同様で、 \begin{align*} w = \alpha^z = e^{z\mathbb{Log}_e{\alpha}} \end{align*} が主値である。

$\square$ 主値にまつわる性質

主値には面白い性質がある。

$\bullet$ 偏角関数

偏角関数に関しては \begin{align*} & \arg(zw) = \arg(z) + \arg(w) \quad\text{であるけれども}\\ & \text{必ずしも} \quad Arg(zw) = Arg(z) + Arg(w) \quad\text{であるとはかぎらない} \end{align*} という事実があるのである。 主値条件として $0 \leq Arg(\cdot) \lt 2\pi$ を採用することにして、$z = w = e^{i\cdot\pi}$ を考えると、まず \begin{align*} Arg(z) = Arg(w) = \pi \;, \quad\therefore\; Arg(z) + Arg(w) = 2\pi \end{align*} となる。 一方で、$zw = e^{i\cdot \pi}e^{i\cdot \pi} = e^{i\cdot 2\pi}$ であるから、 \begin{align*} \arg(zw) = \set{2\pi + 2k\pi \mid k \in \mathbb{z}} \end{align*} であり、偏角の主値の定義とここで採用した主値条件から \begin{align*} & Arg(zw) \in \set{\arg(zw)} \;,\quad 0 \leq Arg{(zw)} \lt 2\pi \\ &\therefore\;\; Arg(zw) = 0 \end{align*} となる（剰余演算（mod 演算？）のような感覚である）。 この結果から \begin{align*} & \text{必ずしも} \quad Arg(zw) = Arg(z) + Arg(w) \quad\text{であるとはかぎらない} \end{align*} ということになる。

$\bullet$ 複素対数関数

複素対数関数についても \begin{align*} & \mathbb{log}_e{(\eta\mu)} = \mathbb{log}_e{\eta} + \mathbb{log}_e{\mu} \quad\text{であるけれども}\\ & \text{必ずしも} \quad \mathbb{Log}_e{(\eta\mu)} = \mathbb{Log}_e{(\eta)} + \mathbb{Log}_e{(\mu)} \quad\text{であるとはかぎらない。} \end{align*} という事実がある。 実際 \begin{align*} \mathbb{Log}_e \eta + \mathbb{Log}_e \mu &= \log_e\abs{\eta} + i\cdot Arg{(\eta)} + \log_e\abs{\mu} + i\cdot Arg{(\mu)} \\ &= \log_e\abs{\eta\mu} + i\cdot\left(Arg{(\eta)} + Arg{(\mu)}\right) \end{align*} であり、他方 \begin{align*} \mathbb{Log}_e (\eta\mu) = \log_e\abs{\eta\mu} + i\cdot Arg{(\eta\mu)} \end{align*} である。 そして上の偏角のところで見たように、この両者の $Arg$ は等しくないことがある。 したがって \begin{align*} \text{必ずしも} \quad \mathbb{Log}_e{(\eta\mu)} = \mathbb{Log}_e{(\eta)} + \mathbb{Log}_e{(\mu)} \quad\text{であるとはかぎらない。} \end{align*} のである。

$\bullet$ $\mathbb{log}_e$ と $\mathbb{Log}_e$

最後に　$\mathbb{log}_e$ と $\mathbb{Log}_e$ に関してである。 ここにも \begin{align*} &\mathbb{log}_e{e^z} = z + i\cdot 2k\pi \quad(k \in \mathbb{Z}) \\ &\mathbb{Log}_e{e^z} = z \end{align*} という違いが存在する。 $z = x + iy$ とすると $e^z = e^{x+iy} = e^x e^{iy}$ であるから \begin{align*} \mathbb{log}_e{e^z} &= \log_e{\abs{e^z}} + i\cdot \arg{(e^z)} = \log_e{e^x} + i\cdot (y + 2k\pi) \\ &= x + iy + i\cdot 2k\pi = z + i\cdot 2k\pi \end{align*} となるけれども、主値の場合は、 \begin{align*} \mathbb{Log}_e{e^z} = \log_e{\abs{e^z}} + i\cdot Arg{(e^z)} = \log_e{e^x} + i\cdot y = x + iy = z \end{align*} なのである。

さて、わざわざ $Arg(z)$ という主値を導入してすべてを１価関数にしたのだから、それをつらぬいて面倒な多価関数を追い出すことを考えればいいのでは？というもっともな疑問が生じてくる。 ところが、今しがた見たように、主値で貫くと、今度は対数関数の「和を積に変える（逆も然り）」という大事な性質を放棄しなくてはいけなくなる。 それゆえ、主値で貫く主値主義よりは、多価関数を認める方がなにかと都合がいいのではあるまいかと想像している。

---

脚註

---

あとがき

冒頭でも記したけれど、本稿は 『指数法則再考』 から派生した雑文である。 その両者において大変お世話になったものが２つあるので、その『指数法則再考』から引用してお礼にかえたい：

複素数の世界については、Internet 上の 新潟大学工学部のこのページのコンテンツ（URL は http://www.eng.niigata-u.ac.jp/~nomoto/2.html） に大変お世話になった。 新しい発見がたくさんあり、とても良い勉強になった。 著者のお名前にたどり着けなかったのでこのような紹介になってしまっている。 失礼があればお許しいただきたい。 あわせて、山本直樹著『複素関数論の基礎』（裳華房、第4版第1刷（2019））もよく紐解いた。 とりわけ複素数というものを曖昧にとらえていたわたくしが、複素数と複素関数の基礎について再度考える際に、とてもためになる本であった。

---