「田崎晴明 著 統計力学1 培風館」 のスターリングの公式の証明に使われている不等式(P.273, A.2.5) \begin{equation} \int_{k-1}^kdx \log x \leq \log k \leq \int_k^{k+1}dx \log x \end{equation} が、一見不思議に思えたので、計算をしてみた。結論。「1」に尽きる。
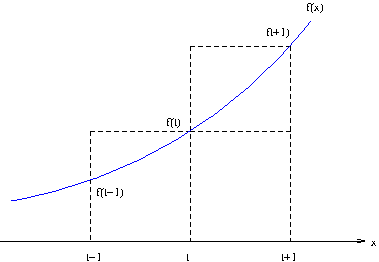
次の式を考えよう。ただし、$f(x)$ は(考えている区間で)単調増加関数であり、かつ、$f(x) \geq 0$ であるものとする。 \begin{equation} \int_{t-1}^tf(x)\,dx \leq f(t) \leq \int_t^{t+1}f(x)\,dx \tag{1} \end{equation} 積分をしているのに、その被積分関数 $f(x)$ をはさんでの大小関係が示されている。 一見したところ、ちょっと奇妙に感じた。 しかし、1 のご利益を考えると、上記 (1) はきちんと証明されるのである。次の図を見てみよう。

そして、積分は「はさまれた区間の面積」であることを思い出し、$f(t)$ を高さの辺とする長方形(もう一つの辺は長さ 1)の面積を比べると、明かに、 \begin{equation} \int_{t-1}^tf(x)\,dx \leq f(t) \times 1 \end{equation} である。同様にして、$t$ から $t+1$ をみてみると、 \begin{equation} f(t) \times 1 \leq \int_t^{t+1}f(x)\,dx \end{equation} がわかる。したがって、先の (1) つまり、 \begin{equation} \int_{t-1}^tf(x)\,dx \leq f(t) \leq \int_t^{t+1}f(x)\,dx \notag \end{equation} であることが、$f(x)$ が単調増加である場合に証明された。 単調増加でない場合にはこれが成り立たないのは、面積に思いを馳せれば、自明と言ってよいだろう。 これから、スターリングの公式までの道程は、上記の本に丁寧に記述されている。
さてさて。上記において、$f(x) \geq 0$ というわりと強い条件を付して説明をしたけれども、もう少しこれを一般化できないものだろうか、と考えてみる。 全く逆のの条件、つまり、$f(x) \leq 0$ の場合をみてみると、グラフのイメージは、
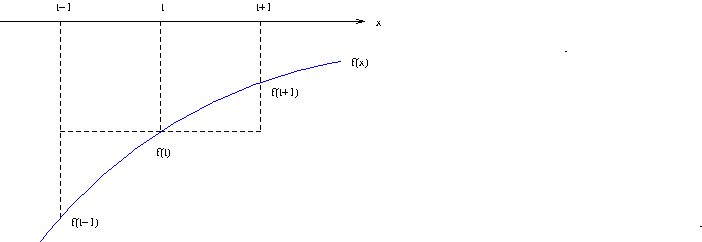
のような感じになる。 ここで天真爛漫に「面積」つまり領域の大きさでみてみると逆の結果になるのだけれども、これは関数なのであった。 つまり、囲まれた部分の値はマイナスの値なのである。 各々の関数値 $f(x)$ はマイナスであるので、区分求積的に計算(積分)をするとその合計値もマイナスである。 したがって、領域の大きさ(面積)が大きいほどその合計値は小さい。 それゆえ、先の大小関係 $\int_{t-1}^tf(x)\,dx \leq f(t) \leq \int_t^{t+1}f(x)\,dx$ も問題なく成立している。 グラフからも明かである。
では、$f(x)$ に単調増加以外の条件がついていない場合はどうだろうか? この場合には、$x$ 軸を横切る際、$f(t)$ の値によって、次の2つのパターンがあることになる。

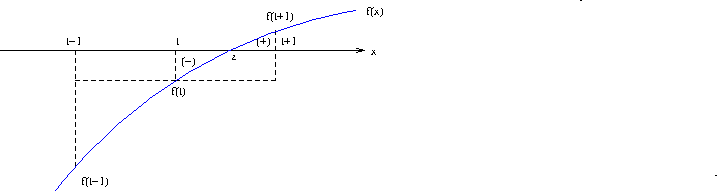
ここでも領域の大きさ(面積)と関数値による区分求積の考えを適用すればいい。 グラフの中の長方形と、(-), (+) で示した部分を見て正負を含めて比べれば、やはり、先の大小関係も成り立っていることがわかる。
最後に蛇足。単調減少関数の場合は? と言っても、ここまでくればもはや自明で、上と同じようにグラフを書いて比べれば良い。単調減少関数を g(x) として、 \begin{equation} \int_{t-1}^tg(x)\,dx \geq g(t) \geq \int_t^{t+1}g(x)\,dx \end{equation} という結果を得る。 少し技巧的にやれば、$f(x)$ を単調増加関数とすれば、$g(x) = -f(x)$ は単調減少関数となるので、 \begin{align*} \int_{t-1}^tf(x)\,dx \leq f(t) \leq \int_t^{t+1}f(x)\,dx &\quad\Longleftrightarrow\quad \int_{t-1}^t -g(x)\,dx \leq -g(t) \leq \int_t^{t+1} -g(x)\,dx \\ &\quad\Longleftrightarrow\quad \int_{t-1}^t g(x)\,dx \geq g(t) \geq \int_t^{t+1} g(x)\,dx \end{align*} となる。
式変形で戯れるのも一興ではあるけれど、やはりグラフのイメージが大切であるし、何より、直感的であるのが良い。